Метод главных компонент - Психологический онлайн-журнал "Родник"

Содержание

Выбор количества точек хранения
Оценка числа главных компонент по правилу сломанной трости
Процесс прогнозирования тестовых данных
Непараметрическая статистика
Источники информации
Примеры анализа данных размерностей
Данные специального вида
Нагрузки
Пределы применимости и ограничения эффективности метода
Графики счетов
Исследование данных
Вычисление счетов и нагрузок
Пример
Примеры кода
Пример кода scikit-learn
Пример на языке R
Неединственность PCA
Пределы применимости и ограничения эффективности метода
Погрешности
Формальная постановка задачи
Аппроксимация данных линейными многообразиями
Поиск ортогональных проекций с наибольшим рассеянием
Поиск ортогональных проекций с наибольшим среднеквадратичным расстоянием между точками
Аннулирование корреляций между координатами
«Качество» декомпозиции
Нагрузки
Графики счетов
Подготовка данных

Выбор количества точек хранения

Существует два способа выбрать необходимое количество компонентов для хранения. Оба метода основаны на отношениях между собственными значениями. Для этого рекомендуется построить график значений. Если точки на графике имеют тенденцию выравниваться и достаточно близки к нулю, то их можно игнорировать. Ограничивают количество компонентов до числа, на которое приходится определенная доля общей дисперсии. Например, если пользователя удовлетворяет 95% от общей дисперсии — получают количество компонентов (VAF) 0.95.

Основные компоненты получают проектированием многомерного статистического анализа метода главных компонентов datavectors на пространстве собственных векторов. Это можно сделать двумя способами — непосредственно из TableOfReal без предварительного формирования PCA объекта и затем можно отобразить конфигурацию или ее номера. Выбрать объект и TableOfReal вместе и «Конфигурация», таким образом, выполняется анализ в собственном окружении компонентов.

Если стартовая точка оказывается симметричной матрицей, например, ковариационной, сначала выполняют сокращение до формы, а затем алгоритм QL с неявными сдвигами. Если же наоборот и отправная точка является матрица данных, то нельзя формировать матрицу с суммами квадратов. Вместо этого, переходят от численно более стабильного способа, и образуют разложения по сингулярным значениям. Тогда матрица будет содержать собственные векторы, а квадратные диагональные элементы — собственные значения.

Оценка числа главных компонент по правилу сломанной трости

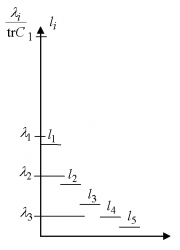
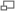
Пример: оценка числа главных компонент по правилу сломанной трости в размерности 5.

Целевой подход к оценке числа главных компонент по необходимой доле объяснённой дисперсии формально применим всегда, однако неявно он предполагает, что нет разделения на «сигнал» и «шум», и любая заранее заданная точность имеет смысл. Поэтому часто более продуктивна иная эвристика, основывающаяся на гипотезе о наличии «сигнала» (сравнительно малая размерность, относительно большая амплитуда) и «шума» (большая размерность, относительно малая амплитуда). С этой точки зрения метод главных компонент работает как фильтр: сигнал содержится, в основном, в проекции на первые главные компоненты, а в остальных компонентах пропорция шума намного выше.

Вопрос, как оценить число необходимых главных компонент, если отношение «сигнал/шум» заранее неизвестно? Одним из наиболее популярных эвристических подходов является правило сломанной трости (англ. Broken stick model)^[1]. Набор нормированных собственных чисел ( $\lambda_i / \tr C$ , $i=1,...,n$ ) сравнивается с распределением длин обломков трости единичной длины, сломанной в $n-1$ -й случайно выбранной точке (точки разлома выбираются независимо и равнораспределены по длине трости). Пусть $L_i$ ( $i=1,...,n$ ) — длины полученных кусков трости, занумерованные в порядке убывания длины: $L_1 \geq L_2 \geq \ldots \geq L_n$ . Нетрудно найти математическое ожидание $L_i$ :

$l_i=\operatorname{E}(L_i)=\frac{1}{n}\sum_{j=i}^{n} \frac{1}{j}.$

По правилу сломанной трости -й собственный вектор (в порядке убывания собственных чисел ) сохраняется в списке главных компонент, если

$\frac{\lambda_1}{\tr C}>l_1 \& \frac{\lambda_2}{\tr C}>l_2 \& \ldots \& \frac{\lambda_k}{\tr C}>l_k.$ l_1 \& \frac{\lambda_2}{\tr C}>l_2 \& \ldots \& \frac{\lambda_k}{\tr C}>l_k.»>

На Рис. приведён пример для 5-мерного случая:

$l_1$ =(1+1/2+1/3+1/4+1/5)/5; $l_2$ =(1/2+1/3+1/4+1/5)/5; $l_3$ =(1/3+1/4+1/5)/5; $l_4$ =(1/4+1/5)/5; $l_5$ =(1/5)/5.

Для примера выбрано

$\frac{\lambda_1}{\tr C}$ =0.5; $\frac{\lambda_2}{\tr C}$ =0.3; $\frac{\lambda_3}{\tr C}$ =0.1; $\frac{\lambda_4}{\tr C}$ =0.06; $\frac{\lambda_5}{\tr C}$ =0.04.

По правилу сломанной трости в этом примере следует оставлять 2 главных компоненты:

$\frac{\lambda_1}{\tr C}>l_1 \;; \; \frac{\lambda_2}{\tr C}>l_2 \;; \;\frac{\lambda_3}{\tr C}<l_3\;.$ l_1 \;; \; \frac{\lambda_2}{\tr C}>l_2 \;; \;\frac{\lambda_3}{\tr C}

Процесс прогнозирования тестовых данных

После того как вычислены главные компоненты начинают процесс прогнозирования тестовых данных с их использованием. Процесс метода главных компонент для чайников прост.

Например, необходимо сделать преобразование в тестовый набор, включая функцию центра и масштабирования в языке R (вер.3.4.2) и его библиотеке rvest. R — свободный язык программирования для статистических вычислений и графики. Он был реконструирован в 1992 году для решения статистических задач пользователями. Это полный процесс моделирования после извлечения PCA.

Набор данных Python:

Для реализации PCA в python импортируют данные из библиотеки sklearn. Интерпретация остается такой же, как и пользователей R. Только набор данных, используемый для Python, представляет собой очищенную версию, в которой отсутствуют вмененные недостающие значения, а категориальные переменные преобразуются в числовые. Процесс моделирования остается таким же, как описано выше для пользователей R. Метод главных компонент, пример расчета:

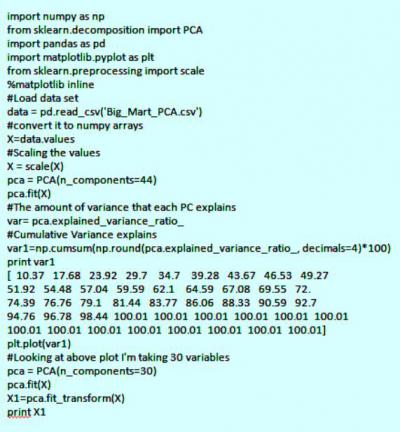
Непараметрическая статистика

Метод главных компонент для непараметрических данных относится к методам измерения, в которых данные извлекаются из определенного распределения. Непараметрические статистические методы широко используются в различных типах исследований. На практике, когда предположение о нормальности измерений не выполняется, параметрические статистические методы могут приводить к вводящим в заблуждение результатам. Напротив, непараметрические методы делают гораздо менее строгие предположения о распределении по измерениям.

Они являются достоверными независимо от лежащих в их основе распределений наблюдений. Из-за этого привлекательного преимущества для анализа различных типов экспериментальных конструкций было разработано много разных типов непараметрических тестов. Такие проекты охватывают дизайн с одной выборкой, дизайн с двумя образцами, дизайн рандомизированных блоков. В настоящее время непараметрический байесовский подход с применением метода главных компонентов используется для упрощения анализа надежности железнодорожных систем.

Железнодорожная система представляет собой типичную крупномасштабную сложную систему с взаимосвязанными подсистемами, которые содержат многочисленные компоненты. Надежность системы сохраняется за счет соответствующих мер по техническому обслуживанию, а экономичное управление активами требует точной оценки надежности на самом низком уровне. Однако данные реальной надежности на уровне компонентов железнодорожной системы не всегда доступны на практике, не говоря уже о завершении. Распределение жизненных циклов компонентов от производителей часто скрывается и усложняется фактическим использованием и рабочей средой. Таким образом, анализ надежности требует подходящей методологии для оценки времени жизни компонента в условиях отсутствия данных об отказах.

Метод главных компонент в общественных науках используется для выполнения двух главных задач:

анализа по данным социологических исследований;
построения моделей общественных явлений.

Источники информации

machinelearning.ru — Метод главных компонент
Лекция «Регрессионный анализ и метод главных компонентов» — К.В. Воронцов, курс «Машинное обучение» 2014
PCA — курс ML Texas A&M University
Principal Component Analysis — статья про Principal Component Analysis в Wikipedia
Understanding PCA

Примеры анализа данных размерностей

Можно рассмотреть метод главных компонентов на примере выполнения симметричной корреляционной или ковариационной матрицы. Это означает, что матрица должна быть числовой и иметь стандартизованные данные. Допустим, есть набор данных размерностью 300 (n) × 50 (p). Где n — представляет количество наблюдений, а p — число предикторов.

Поскольку имеется большой p = 50, может быть p(p-1)/2 диаграмма рассеяния. В этом случае было бы хорошим подходом выбрать подмножество предиктора p (p<< 50), который фиксирует количество информации. Затем следует составление графика наблюдения в полученном низкоразмерном пространстве. Не следует забывать, что каждое измерение является линейной комбинацией р-функций.

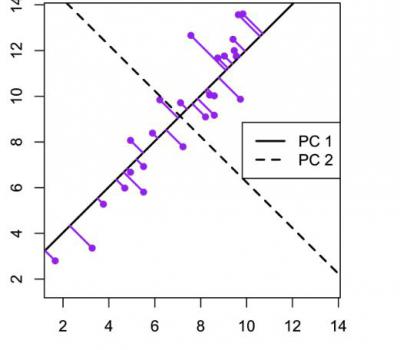
Пример для матрицы с двумя переменными. В этом примере метода главных компонентов создается набор данных с двумя переменными (большая длина и диагональная длина) с использованием искусственных данных Дэвиса.

Компоненты можно нарисовать на диаграмме рассеяния следующим образом.

Этот график иллюстрирует идею первого или главного компонента, обеспечивающего оптимальную сводку данных — никакая другая линия, нарисованная на таком графике рассеяния, не создаст набор прогнозируемых значений точек данных на линии с меньшей дисперсией.

Первый компонент также имеет приложение в регрессии с уменьшенной главной осью (RMA), в которой предполагается, что как x-, так и y-переменные имеют ошибки или неопределенности или, где нет четкого различия между предсказателем и ответом.

Данные специального вида

Результат моделирования
методом главных компонент не зависит от
порядка, в котором следуют образцы и/или
переменные. Иными словами строки и
столбцы в исходной матрице X можно
переставить, но ничего принципиально не
изменится. Однако, в некоторых случаях,
сохранять и отслеживать этот порядок
очень полезно – это позволяет лучше
понять устройство моделируемых данных.

Рис.
8 Данные ВЭЖХ–ДДМ

Рассмотрим простой пример –
моделирование данных, полученных
методом высокоэффективной жидкостной
хроматографией с детектированием на
диодной матрице (ВЭЖХ–ДДМ). Данные
представляются матрицей, размерностью 30
образцов (I) на 28 переменных (J).
Образцы соответствуют временам
удерживания от 0 до 30 с, а переменные –
длинам волн от 220 до 350 нм, на которых
происходит детектирование. Данные ВЭЖХ–ДДМ
представлены на Рис 8.

Эти
данные хорошо моделируются методом PCA с
двумя главными компонентами. Ясно, что в
этом примере нам важен порядок, в
котором идут образцы и переменные – он
задается естественным ходом времени и
спектральным диапазоном. Полученные
счета и нагрузки полезно изобразить на
графиках в зависимости от
соответствующего параметра – счета от
времени, а нагрузки от длины волны. (см. Рис
9)

Рис.
9 Графики счетов и нагрузок для данных
ВЭЖХ–ДДМ

Подробнее этот пример разобран в пособии
Разрешение многомерных кривых .

Содержание

Нагрузки

Матрица нагрузок P – это
матрица перехода из исходного
пространства переменных x₁, …x_J
(J-мерного) в пространство главных
компонент (A-мерное). Каждая строка
матрицы P состоит из коэффициентов,
связывающих переменные t и x (1).
Например, a-я строка – это проекция
всех переменных x₁, …x_J
на a-ю ось главных компонент. Каждый
столбец P – это проекция
соответствующей переменной x_j
на новую систему координат.

Рис.7
График нагрузок

График нагрузок применяется
для исследования роли переменных. На
этом графике каждая переменная xj
отображается точкой в координатах (pi,
pj), например (p1, p2).
Анализируя его аналогично графику
счетов, можно понять, какие переменные
связаны, а какие независимы. Совместное
исследование парных графиков счетов и
нагрузок, также может дать много
полезной информации о данных.

В
методе главных компонент нагрузки – это
ортогональные нормированные вектора, т.е.

PtP
= I

Для вычисления PCA-нагрузок в
надстройке Chemometrics Add-In
используется функция
LoadingsPCA.

Содержание

Пределы применимости и ограничения эффективности метода

Метод главных компонент применим всегда. Распространённое утверждение о том, что он применим только к нормально распределённым данным (или для распределений, близких к нормальным) неверно: в исходной формулировке К. Пирсона ставится задача об аппроксимации конечного множества данных и отсутствует даже гипотеза о их статистическом порождении, не говоря уж о распределении.

Однако метод не всегда эффективно снижает размерность при заданных ограничениях на точность $E(m)$. Прямые и плоскости не всегда обеспечивают хорошую аппроксимацию. Например, данные могут с хорошей точностью следовать какой-нибудь кривой, а эта кривая может быть сложно расположена в пространстве данных. В этом случае метод главных компонент для приемлемой точности потребует нескольких компонент (вместо одной), или вообще не даст снижения размерности при приемлемой точности.

Больше неприятностей могут доставить данные сложной топологии. Для их аппроксимации также изобретены различные методы, например самоорганизующиеся карты Кохонена ^[4] или нейронный газ ^[5]. Если данные статистически порождены с распределением, сильно отличающимся от нормального, то для аппроксимации распределения полезно перейти от главных компонент к независимым компонентам ^[6], которые уже не ортогональны в исходном скалярном произведении. Наконец, для изотропного распределения (даже нормального) вместо эллипсоида рассеяния получаем шар, и уменьшить размерность методами аппроксимации невозможно.

Графики счетов

Посмотрим на графики счетов,
которые показывают, как расположены
образцы в проекционном пространстве.

На
графике младших счетов PC1–PC2 (Рис.
21) мы видим четыре отдельные группы,
разложенные по четырем квадрантам:
слева – женщины (F), справа – мужчины (M),
сверху – юг (S), а снизу – север (N). Из этого
сразу становится ясен смысл первых двух
направлений PC1 и PC2. Первая компонента
разделяет людей по полу, а вторая – по
месту жительства. Именно эти факторы
наиболее сильно влияют на разброс
свойств.

Рис.
21 График счетов (PC1 – PC2) с обозначениями,
использованными ранее на Рис 16

Продолжим
изучение, построив график старших
счетов PC3– PC4 (Рис. 22 ).

Рис.
22 График счетов (PC3 – PC4) с новыми
обозначениями:
размер и цвет символов отражает доход –
чем больше и светлее, тем он больше.
Числа представляют возраст

Здесь
уже не видно таких отчетливых групп. Тем
не менее, внимательно исследовав этот
график совместно с таблицей исходных
данных, можно, после некоторых усилий,
сделать вывод о том, что PC3 отделяет
старых/богатых людей от молодых/бедных.
Чтобы сделать это более очевидным, мы
изменили обозначения. Теперь каждый
человек показан кружком, цвет и размер
которого меняется в зависимости от
дохода – чем больше и светлее, тем больше
доход. Рядом показан возраст каждого
объекта. Как видно, возраст и доход
уменьшается слева направо, т.е. вдоль PC3.
А вот смысл PC4 нам по–прежнему не ясен.

Содержание

Исследование данных

Прежде всего, любопытно
посмотреть на графиках, как связаны
между собой все эти переменные. Зависит
ли рост (Height ) от веса (Weight)?
Отличаются ли женщины от мужчин в
потреблении вина (Wine)? Связан ли
доход (Income) с возрастом (Age)?
Зависит ли вес (Weight) от потребления
пива (Beer)?

Рис.
16 Связи между переменными в примере People.
Женщины (F) обозначены кружками ●
и ●,
а мужчины (M) – квадратами ■
и ■.
Север (N) представлен голубым ■,
а юг (S) – красным цветом ●.

Некоторые из этих зависимостей
показаны на Рис.16. Для
наглядности на всех графиках
использованы одни и те же обозначения:
женщины (F) показаны кружками, мужчины (M) –
квадратами, север (N) представлен голубым,
а юг (S) – красным цветом.

Связь
между весом (Weight) и ростом (Height)
показана на Рис.16a. Очевидна, прямая (положительная)
пропорциональность. Учитывая
маркировку точек, можно заметить также,
что мужчины (M) в большинстве своем
тяжелее и выше женщин (F).

На Рис. 16b показана другая пара
переменных: вес (Weight) и пиво (Beer).
Здесь, помимо очевидных фактов, что
большие люди пьют больше, а женщины –
меньше, чем мужчины, можно заметить еще
две отдельные группы – южан и северян.
Первые пьют меньше пива при том же весе.

Эти же группы заметны и на Рис.16c,
где показана зависимость между
потреблением вина (Wine) и пива (Beer).
Из него видно, что связь между этими
переменными отрицательна – чем больше
потребляется пива, тем меньше вина. На
юге пьют больше вина, а на севере – пива.
Интересно, что в обеих группах женщины
располагаются слева, но не ниже по
отношению к мужчинам. Это означает, что,
потребляя меньше пива, прекрасный пол
не уступает в вине.

Последний график на Рис. 16d
показывает, как связаны возраст (Age)
и доход (Income). Легко видеть, что даже
в этом сравнительно небольшом наборе
данных есть переменные, как с
положительной, так и с отрицательной
корреляцией.

Можно ли
построить графики для всех пар
переменных выборки? Вряд ли. Проблема состоит в том, что для 12 переменных
существует 12(12–1)/2=66 таких комбинаций.

Содержание

Вычисление счетов и нагрузок

Для построения PCA декомпозиции
можно воспользоваться стандартными
функциями ScoresPCA
и LoadingsPCA,
имеющимися в надстройке Chemometrics. Мы
вычислим все 12 возможных главных
компонент. В качестве первого аргумента
используется исходный, не
преобразованный массив данных, поэтому
последний аргумент в обеих функциях
равен 3 – автошкалирование.

Рис.
19 Вычисление матрицы счетов

Рис.
20 Вычисление матрицы нагрузок

В
этом пособии все PCA вычисления
проводятся в книге People.xls на листе
MVA.
Для удобства читателя эти же результаты
продублированы на листе PCA
как числа, без ссылки на надстройку Chemometrics.xla.
Остальные листы рабочей книги связаны
не с данными на листе MVA, с данными на
листе PCA. Поэтому файл People.xls можно
использовать даже тогда, когда
надстройка Chemometrics.xla не установлена на компьютере.

Содержание

Пример

Метод главных компонент
иллюстрируется примером, помещенным в
файл People.xls.

Этот
файл включает в себя следующие листы:

Intro:
краткое введение

Layout:
схемы, объясняющая имена массивов,
используемых в примере

Data: данные,
используемые в примере.

MVA:
PCA декомпозиция, выполненная с помощью
надстройки Chemometrics.xla

PCA: копия
всех результатов PCA не привязанная к
надстройке Chemometrics.xla

Scores1–2:
анализ младших счетов PC1–PC2

Scores3–4:
анализ старших счетов PC3–PC4

Loadings:
анализ нагрузок

Residuals:
анализ остатков

Содержание

Примеры кода

Пример кода scikit-learn

Пример применения PCA к датасету Iris для уменьшения размерности:

 # Импорт библиотек
 import numpy as np
 import matplotlib.pyplot as plt
 from sklearn import decomposition
 from sklearn import datasets

 # Загрузка данных
 centers = [[1, 1], [-1, -1], [1, -1]]
 iris = datasets.load_iris()
 X = iris.data
 y = iris.target

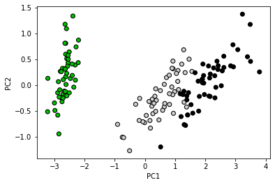
Применения PCA к датасету Iris

 # Преобразование данных датасета Iris, уменьшающее размерность до 2
 pca = decomposition.PCA(n_components=3)
 pca.fit(X)
 X = pca.transform(X)
 y = np.choose(y, [1, 2, 0]).astype(np.float)
 plt.clf()
 plt.cla()
 plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.nipy_spectral, edgecolor='k')
 plt.xlabel("PC1")
 plt.ylabel("PC2")
 plt.show()

Пример на языке R

# importing library and its' dependencies
library(h2o)
h2o.init()

path <- system.file(, ,  = )
data <- h2o.uploadFile( = data)


h2o.prcomp( = data,  = ,  = )

Неединственность PCA

Разложение по методу главных
компонент

не
является единственным. Вместо матриц T
и P можно использовать другие
матрицы
и
,
которые дадут аналогичную декомпозицию

с
той же матрицей ошибок E. Простейший
пример – это одновременное изменение
знаков у соответствующих компонент
векторов ta и pa,
при котором произведение

остается
неизменным. Алгоритм NIPALS дает именно
такой результат – с точностью до знака,
поэтому его реализация в разных
программах может приводить к
расхождениям в направлениях главных
компонент.

Более сложный случай
– это одновременное вращение матриц T
и P. Пусть R – это ортогональная
матрица вращения размерностью A×A , т.е такая
матрица, что Rt=R–1.
Тогда

Заметим,
что новые матрицы счетов и нагрузок
сохраняют все свойства старых,

Это
свойство PCA называется вращательной
неопределенностью. Оно интенсивно
используется при решении задач
разделения кривых, в частности
методом прокрустова
вращения. Если отказаться от условий
ортогональности главных компонент, то
декомпозиция матрицы станет еще более
общей. Пусть теперь R – это
произвольная невырожденная матрица
размерностью A×A . Тогда

Эти
матрицы счетов и нагрузок уже не
удовлетворяют условию ортогональности
и нормирования. Зато они могут состоять
только из неотрицательных элементов, а
также подчиняться другим требованиям,
накладываемым при решении задач
разделения сигналов.

Содержание

Пределы применимости и ограничения эффективности метода

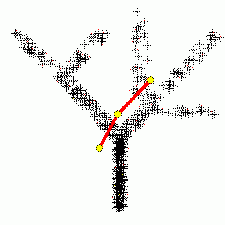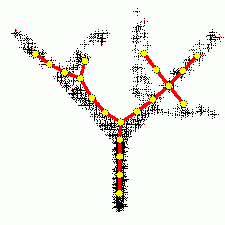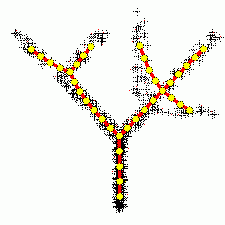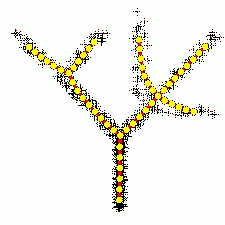
Построение ветвящихся главных компонент методом топологических грамматик. Крестики — точки данных, красное дерево с желтыми узлами — аппроксимирующий дендрит^[1].

Однако метод не всегда эффективно снижает размерность при заданных ограничениях на точность $\delta_k$ . Прямые и плоскости не всегда обеспечивают хорошую аппроксимацию. Например, данные могут с хорошей точностью следовать какой-нибудь кривой, а эта кривая может быть сложно расположена в пространстве данных. В этом случае метод главных компонент для приемлемой точности потребует нескольких компонент (вместо одной), или вообще не даст снижения размерности при приемлемой точности. Для работы с такими «кривыми» главными компонентами изобретен метод главных многообразий^[1] и различные версии нелинейного метода главных компонент^[1]^[1]. Больше неприятностей могут доставить данные сложной топологии. Для их аппроксимации также изобретены различные методы, например самоорганизующиеся карты Кохонена, нейронный газ^[1] или топологические грамматики^[1]. Если данные статистически порождены с распределением, сильно отличающимся от нормального, то для аппроксимации распределения полезно перейти от главных компонент к независимым компонентам^[1], которые уже не ортогональны в исходном скалярном произведении. Наконец, для изотропного распределения (даже нормального) вместо эллипсоида рассеяния получаем шар, и уменьшить размерность методами аппроксимации невозможно.

Погрешности

PCA декомпозиция матрицы X
является последовательным, итеративным
процессом, который можно оборвать на
любом шаге a=A. Получившаяся
матрица

вообще
говоря, отличается от матрицы X. Разница
между ними

называется
матрицей остатков.

Рассмотрим
геометрическую интерпретацию остатков.
Каждый исходный образец xi (строка
в матрице X) можно представить как
вектор в J– мерном пространстве с
координатами

Рис.
10 Геометрия PCA

PCA проецирует его в вектор,
лежащий в пространстве главных
компонент, t_i=(t_i1,
t_i2, …t_iA)
размерностью A. В исходном
пространстве этот же вектор t_i
имеет координаты

Разница
между исходным вектором и его проекцией
является вектором остатков

Он
образует i–ю строку в матрице
остатков E.

Рис.11
Вычисление остатков

Исследуя остатки можно понять,
как устроены данные и хорошо ли они
описываются PCA моделью.

Для вычисления
PCA-остатков можно использовать приемы, описанные в
пособии Расширение возможностей Chemometrics Add-In.

Величина
–

определяет
квадрат отклонения исходного вектора xi от его проекции
на пространство PC. Чем оно меньше, тем
лучше приближается i–ый образец.

Для
вычисления отклонений можно использовать стандартные
функции листа или специальную пользовательскую
функцию.

Эта
же величина, деленная на число
переменных

дает
оценку дисперсии (вариации) i–го
образца.

Среднее (для всех
образцов) расстояние v0
вычисляется как

Оценка общая (для всех образцов) дисперсии вычисляется так –

Содержание

Формальная постановка задачи

Задача анализа главных компонент, имеет, как минимум, четыре базовых версии:

аппроксимировать данные линейными многообразиями меньшей размерности;
найти подпространства меньшей размерности, в ортогональной проекции на которые разброс данных (т.е. среднеквадратичное уклонение от среднего значения) максимален;
найти подпространства меньшей размерности, в ортогональной проекции на которые среднеквадратичное расстояние между точками максимально;
для данной многомерной случайной величины построить такое ортогональное преобразование координат, что в результате корреляции между отдельными координатами обратятся в ноль.

Первые три версии оперируют конечными множествами данных. Они эквивалентны и не используют никакой гипотезы о статистическом порождении данных. Четвёртая версия оперирует случайными величинами. Конечные множества появляются здесь как выборки из данного распределения, а решение трёх первых задач — как приближение к «истинному» преобразованию Кархунена-Лоэва. При этом возникает дополнительный и не вполне тривиальный вопрос о точности этого приближения.

Аппроксимация данных линейными многообразиями

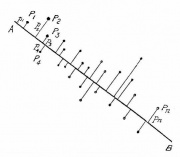
Метод главных компонент начинался с задачи наилучшей аппроксимации конечного множества точек прямыми и плоскостями (К. Пирсон, 1901). Дано конечное множество векторов . Для каждого среди всех -мерных линейных многообразий в найти такое , что сумма квадратов уклонений от минимальна:

$\sum_{i=1}^m \operatorname{dist}^2(x_i, L_k) \to \min$ ,

где — евклидово расстояние от точки до линейного многообразия. Всякое -мерное линейное многообразие в может быть задано как множество линейных комбинаций , где параметры пробегают вещественную прямую , а — ортонормированный набор векторов

$\operatorname{dist}^2(x_i, L_k) = \| x_i - a_0 - \sum_{j=1}^k a_j (a_j, x_i - a_0) \| ^2$ ,

где евклидова норма, — евклидово скалярное произведение, или в координатной форме:

$\operatorname{dist}^2(x_i, L_k) = \sum_{l=1}^n \left(x_{il} - a_{0l}- \sum_{j=1}^k a_{jl} \sum_{q=1}^n a_{jq}(x_{iq} - a_{0q}) \right)^2$ .

Решение задачи аппроксимации для даётся набором вложенных линейных многообразий , . Эти линейные многообразия определяются ортонормированным набором векторов (векторами главных компонент) и вектором .
Вектор ищется, как решение задачи минимизации для :

$a_0 = \underset{a_0\in\mathbb{R}^n}{\operatorname{argmin}} \left(\sum_{i=1}^m \operatorname{dist}^2(x_i, L_0)\right),$

то есть

$a_0 = \underset{a_0\in\mathbb{R}^n}{\operatorname{argmin}} \left (\sum_{i=1}^m \| x_i - a_0\| ^2\right)$ .

Это — выборочное среднее:
Фреше в 1948 году обратил внимание, что вариационное определение среднего (как точки, минимизирующей сумму квадратов расстояний до точек данных) очень удобно для построения статистики в произвольном метрическом пространстве, и построил обобщение классической статистики для общих пространств (обобщённый метод наименьших квадратов).

Векторы главных компонент могут быть найдены как решения однотипных задач оптимизации:

1) централизуем данные (вычитаем среднее): $x_i:= x_i - \overline{X_i}$ . Теперь $\sum_{i=1}^m x_i =0$ ;

2) находим первую главную компоненту как решение задачи;

$a_1 = \underset{\| a_1 \| =1}{\operatorname{argmin}} \left( \sum_{i=1}^m \| x_i - a_1 (a_1,x_i)\| ^2\right)$ .

Если решение не единственно, то выбираем одно из них.

3) Вычитаем из данных проекцию на первую главную компоненту:

$x_i:= x_i - a_1 \left(a_1,x_i\right)$ ;

4) находим вторую главную компоненту как решение задачи

$a_2 = \underset{\| a_2 \| =1}{\operatorname{argmin}} \left( \sum_{i=1}^m \| x_i - a_2 (a_2,x_i)\| ^2\right)$ .

Если решение не единственно, то выбираем одно из них.

…

2k-1) Вычитаем проекцию на $(k-1)$ -ю главную компоненту (напомним, что проекции на предшествующие $(k-2)$ главные компоненты уже вычтены):

$x_i:= x_i - a_{k-1} \left(a_{k-1},x_i\right)$ ;

2k) находим k-ю главную компоненту как решение задачи:

$a_k = \underset{\| a_k \| =1}{\operatorname{argmin}} \left( \sum_{i=1}^m \| x_i - a_k (a_k,x_i)\| ^2\right)$ .

Если решение не единственно, то выбираем одно из них.

…

На каждом подготовительном шаге вычитаем проекцию на предшествующую главную компоненту. Найденные векторы ортонормированы просто в результате решения описанной задачи оптимизации, однако чтобы не дать ошибкам вычисления нарушить взаимную ортогональность векторов главных компонент, можно включать в условия задачи оптимизации.

Неединственность в определении помимо тривиального произвола в выборе знака ( и решают ту же задачу) может быть более существенной и происходить, например, из условий симметрии данных.

Поиск ортогональных проекций с наибольшим рассеянием

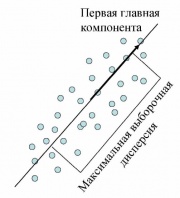
Первая главная компонента максимизирует выборочную дисперсию проекции данных

Пусть нам дан центрированный набор векторов данных (среднее арифметическое значение равно нулю). Задача — найти такое ортогональное преобразование в новую систему координат, для которого были бы верны следующие условия:

Выборочная дисперсия данных вдоль направления, заданного нормированным вектором , это

$S^2_m \left[ (X, a_k) \right ] = \frac{1}{m} \sum\limits_{i=1}^m \left(\sum\limits_{j=1}^n x_{ij}a_{kj} \right)^2$

(поскольку данные центрированы, выборочная дисперсия здесь совпадает со средним квадратом уклонения от нуля).

Формально, если , — искомое преобразование, то для векторов должны выполняться следующие условия:

$a_1 = \underset{\| a_1 \| =1}{\operatorname{argmax}}\,S^2_m \left [(X, a_1) \right ];$

Если решение не единственно, то выбираем одно из них.

Вычитаем из данных проекцию на первую главную компоненту:

$x_i:= x_i-a_1 \left(a_1,x_i\right)$ ; в результате $x_i \bot a_1$ ;

находим вторую главную компоненту как решение задачи

$a_2 = \underset{\| a_2 \| =1}{\operatorname{argmax}}\,S^2_m \left [ (X, a_2) \right ];$

Если решение не единственно, то выбираем одно из них.

$x_i:= x_i-a_{k-1} \left(a_{k-1},x_i\right)$ ; в результате $x_i \bot a_l, (l = 1,\dots k-1)$ ;

находим $k$ -ю главную компоненту как решение задачи

$a_n = \underset{\| a_k\| = 1}{\operatorname{argmax}}\,S^2_m \left [ (X, a_k) \right ];$

Если решение не единственно, то выбираем одно из них.

Фактически, как и для задачи аппроксимации, на каждом шаге решается задача о первой главной компоненте для данных, из которых вычтены проекции на все ранее найденные главные компоненты. При большом числе итерации (большая размерность, много главных компонент) отклонения от ортогональности накапливаются и может потребоваться специальная коррекция алгоритма или другой алгоритм поиска собственных векторов ковариационной матрицы.

Решение задачи о наилучшей аппроксимации даёт то же множество решений , что и поиск ортогональных проекций с наибольшим рассеянием, по очень простой причине: и первое слагаемое не зависит от . Только одно дополнение к задаче об аппроксимации: появляется последняя главная компонента

Поиск ортогональных проекций с наибольшим среднеквадратичным расстоянием между точками

Ещё одна эквивалентная формулировка следует из очевидного тождества, верного для любых векторов :

$\frac{1}{m(m-1)}\sum_{i,j=1}^m (x_i-x_j)^2 =\frac{2m^2}{m(m-1)}\left[\frac{1}{m}\sum_{i=1}^m x_i^2 - \left(\frac{1}{m}\sum_{i}^m x_i \right)^2\right].$

В левой части этого тождества стоит среднеквадратичное расстояние между точками, а в квадратных скобках справа — выборочная дисперсия. Таким образом, в методе главных компонент ищутся подпространства, в проекции на которые среднеквадратичное расстояние между точками максимально (или, что то же самое, его искажение в результате проекции минимально)^[1]. Такая переформулировка позволяет строить обобщения с взвешиванием различных парных расстояний (а не только точек).

Аннулирование корреляций между координатами

Для заданной -мерной случайной величины найти такой ортонормированный базис, , в котором коэффициент ковариации между различными координатами равен нулю. После преобразования к этому базису

$\operatorname{cov}(X_i,X_j)=0$ для $i \neq j$ .

Здесь — коэффициент ковариации.

«Качество» декомпозиции

Результатом PCA моделирования
являются величины
–
оценки, найденные по модели, построенной
на обучающем наборе Xc.
Результатом проверки служат величины
–
оценки проверочных значений Xt,
вычисленные по той же модели, но как
новые образцы (3). Отклонение
оценки от проверочного значения
вычисляют как матрицу остатков: в
обучении

и
в проверке

Следующие
величины характеризуют «качество»
моделирования в среднем.

Полная
дисперсия остатков в обучении (TRVC) и в
проверке (TRVP) –

Полная дисперсия выражается в
тех же единицах (точнее их квадратах),
что и исходные величины X.

Объясненная
дисперсия остатков в обучении (ERVC) и в
проверке (ERVP)

Объясненная дисперсия – это
относительная величина. При ее
вычислении используется естественная
нормировка – сумма квадратов всех
исходных величин xij. Обычно
она выражается в процентах или в долях
единицы. Во всех этих формулах величины eij
– это элементы матриц Ec или Et.
Для характеристик, наименование которых
оканчивается на C (например, TRVC),
используется матрица Ec (обучение),
а для тех, которые оканчиваются на P (например,
TRVP), берется матрица Et (проверка).

Содержание

Нагрузки

Рис.7
График нагрузок

В
методе главных компонент нагрузки – это
ортогональные нормированные вектора, т.е.

PtP
= I

Для вычисления PCA-нагрузок в
надстройке Chemometrics Add-In
используется функция
LoadingsPCA.

Содержание

Графики счетов

Посмотрим на графики счетов,
которые показывают, как расположены
образцы в проекционном пространстве.

Рис.
21 График счетов (PC1 – PC2) с обозначениями,
использованными ранее на Рис 16

Продолжим
изучение, построив график старших
счетов PC3– PC4 (Рис. 22 ).

Содержание

Подготовка данных

Во многих случаях, перед
применением PCA, исходные данные нужно
предварительно подготовить:
отцентрировать и/или отнормировать. Эти
преобразования проводятся по столбцам –
переменным.

Центрирование
– это вычитание из каждого столбца xj
среднего (по столбцу) значения

Центрирование
необходимо потому, что оригинальная PCA
модель (2) не содержит
свободного члена.

Второе
простейшее преобразование данных – это нормирование.
Это преобразование выравнивает вклад
разных переменных в PCA модель. При этом
преобразовании каждый столбец xj
делится на свое стандартное отклонение.

Комбинация
центрирования и нормирования по
столбцам называется автошкалированием.

Любое
преобразование данных – центрирование,
нормирование, и т.п. – всегда делается
сначала на обучающем наборе. По этому
набору вычисляются значения mj и
sj, которые затем применяются и
к обучающему, и к проверочному набору.

В надстройке
Chemometrics Add In подготовка данных
проводится автоматически. Если подготовку
нужно провести вручную, то для нее можно использовать
стандартные функции листа или специальную
пользовательскую функцию.

В
задачах, где структура исходных данных X
априори предполагает однородность и
гомоскедастичность, подготовка данных
не только не нужна, но и вредна. Именно
такой случай представляют ВЭЖХ–ДДМ данные,
рассмотренные в пособии Разрешение многомерных кривых.

Содержание